- Ionization Energy Of Hydrogen
- Ionization Energy Of Hydrogen
- Ionization Energy Of Hydrogen Line
- Ionization Energy Of Hydrogen Ev
Professor of Chemistry / McMaster University / Hamilton,Ontario
| ||||||||||||||||||||||||||||||||||||||||
The Quantization of Energy
The energy of an electron in Bohr’s orbit of Hydrogen atom is given by the expression: E n = 2 π 2 m e 4 Z 2 n 2 h 2 (4 π ϵ 0) 2 = − 13.6 Z 2 n 2 e V Since Z = 1 for hydrogen, the above equation can be further simplified. Now just plug in the required values. Ionization of Hydrogen Revision: 1:2 The ionization state of a gas in equilibrium at temperature Tcan be found using Saha’s equation, N j+1 N j = 2Z j+1 n eZ j 2ˇm ekT h2 3=2 e ˜ j=kT: (1) There is a separate Saha equation for each pair (j;j+ 1) of ionization states associated with each element present in the gas. These equations have to be.
The motion of the electron is not free. The electron is bound to theatom by the attractive force of the nucleus and consequently quantum mechanicspredicts that the total energy of the electron is quantized. The expressionfor the energy is:| (1) |
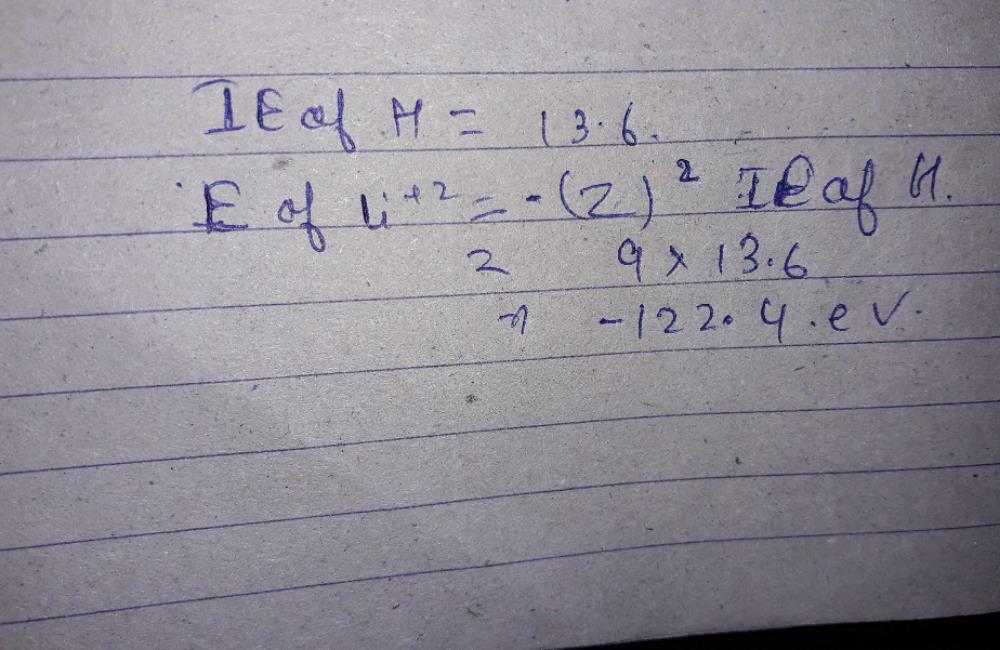
Ionization Energy Of Hydrogen
where m is the mass of the electron, e is the magnitudeof the electronic charge, n is a quantum number, h is Planck'sconstant and Z is the atomic number (the number of positive chargesin the nucleus).
One mole of hydrogen atoms has an atomic weight of 1.00 gram, and the ionization energy is 1,312 kilojoules per mole of hydrogen. The ionization energy is a measure of the capability of an element to enter into chemical reactions requiring ion formation or donation of electrons.
This formula applies to any one-electron atom or ion. Forexample, He+ is a one-electron system for which Z = 2.We can again construct an energy level diagram listing the allowedenergy values (Fig. 3-2).
Fig. 3-2. The energy leveldiagram for the H atom. Each line dentoes an allowed energy for the atom.
These are obtained by substituting all possible values of n intoequation (1)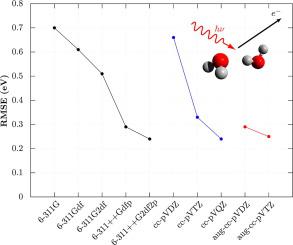
. As in our previous example,we shall represent all the constants which appear in the expression forEnby a constant K and we shall set Z = 1.| (2) |
Since the motion of the electron occurs in three dimensions we mightcorrectly anticipate three quantum numbers for the hydrogen atom. But theenergy depends only on the quantum number n and for this reasonit is called the principal quantum number. In this case,the energy is inversly dependent upon n2,and as n is increased the energy becomes less negative with thespacings between the energy levels decreasing in size. When n =¥, E = 0 and the electron is free of the attractive force ofthe nucleus. The average distance between the nucleus and the electron(the average value of r) increases as the energy or the value ofnincreases. Thus energy must be supplied to pull the electron awayfrom the nucleus.
The parallelism between increasing energy and increasingaverage value of r is a useful one. In fact, when an electron losesenergy, we refer to it as 'falling' from one energy level to a lowerone on the energy level diagram. Since the average distance between thenucleus and the electron also decreases with a decrease in n, thenthe electron literally does fall in closer to the nucleus when it 'falls'from level to level on the energy level diagram.
The energy difference between E¥and E1:
is called the ionization energy. It is the energy required to pull theelectron completely away from the nucleus and is, therefore, the energyof the reaction:
This amount of energy is sufficient to separate the electron from theattractive influence of the nucleus and leave both particles at rest. Ifan amount of energy greater than K is supplied to the electron,it will not only escape from the atom but the energy in excess of Kwill appear as kinetic energy of the electron. Once the electron is freeit may have any energy because all velocities are then possible.This is indicated in the energy level diagram bythe shading above the E¥= 0 line. An electron which possesses and energy in this region of thediagram is a free electron and has kinetic energy of motion only.
The Hydrogen Atom Spectrum
As mentioned earlier, hydrogen gas emits colouredlight when a high voltage is applied across a sample of the gas containedin a glass tube fitted with electrodes. The electrical energy transmittedto the gas causes many of the hydrogen molecules to dissociate into atoms:
The electrons in the molecules and in the atoms absorb energy and areexcited to high energy levels. lonization of the gas also occurs. Whenthe electron is in a quantum level other than the lowest level (with n= 1) the electron is said to be excited, or to be in an excited level.The lifetime of such an excited level is very brief, being of the orderof magnitude of only 10-8 sec. The electronloses the energy of excitation by falling to a lower energylevel and at the same time emitting a photon to carry off the excessenergy. We can easily calculate the frequencies which should appear inthe emitted light by calculating the difference in energy between the twolevels and making use of Bohr's frequency condition:
Suppose we consider all those frequencies which appearwhen the electron falls to the lowest level, n = 1,| (3) |
Every value of n substituted into this equation gives a distinctvalue for v. In Fig. 3-3 we illustrate thechanges in energy which result when the electron emits a photon by an arrowconnecting the excited level (of energy En) with theground level (of energy E1). Thefrequency resulting from each drop in energy will be directly proportionalto the length of the arrow. Just as the arrows increase in length as nis increased, so v increases. However, the spacings between thelines decrease as n is increased, and the spectrum will appear asshown directly below the energy level diagram in Fig.3-3.
Fig. 3-3. The energy changesand corresponding frequencies which give rise to the Lyman series in thespectrum of the H atom. The line spectrum degenerates into a continuousspectrum at the high frequency end.
Each line in the spectrum is placed beneath the arrow which representsthe change in energy giving rise to that particular line. Free electronswith varying amounts of kinetic energy (½mu2)can also fall to the n = 1 level.
The energy released in the reversed ionization reaction:
will equal K, the difference between E¥and E1, plus ½mu2,the kinetic energy originally possessed by the electron. Since this latterenergy is not quantized, every energy value greater than K shouldbe possible and every frequency greater than that corresponding to
Ionization Energy Of Hydrogen
should be observed. The line spectrum should, therefore, collapse intoa continuous spectrum at its high frequency end. Thus the energy continuum above E¥gives rise to a continuum of frequencies in the emission spectrum. The beginning of the continuum should be the frequency corresponding tothe jump from E¥to E1, and thus we can determineK,the ionization energy of the hydrogen atom, from the observation of thisfrequency. Indeed, the spectroscopic method is one of the most accuratemethods of determining ionization energies.
The hydrogen atom does possess a spectrum identical tothat predicted by equation (3), andthe observed value for K agrees with the theoretical value. Thisparticular series of lines, called the Lyman series, falls in the ultravioletregion of the spectrum because of the large energy changes involved inthe transitions from the excited levels to the lowest level. The firstfew members of a second series of lines, a second line spectrum, fallsin the visible portion of the spectrum. It is called the Balmer seriesand arises from electrons in excited levels falling to the second quantumlevel. Since E2 equals only one quarterof E1, the energy jumps are smallerand the frequencies are correspondingly lower than those observed in theLyman series. Four lines can be readily seen in this series: red, green,blue, and violet. Each colour results from the electrons falling from aspecific level, to the n = 2 level: red E3®E2;green, E4®E2; blue, E5®E2;and violet E6®E2.Other series, arising from electrons falling to the n = 3 and n= 4 levels, can be found in the infrared (frequencies preceding the redend or long wavelength end of the visible spectrum).
Ionization Energy Of Hydrogen Line
The fact that the hydrogen atom exhibits aline spectrum is visible proof of the quantization of energy on the atomiclevel.
Ionization Energy Of Hydrogen Ev